（無題）

iPod touchを買いました。
何故この時期にと言われても…
機会があったからとしか言いようがありません。
最新型のiPod touchなので、
デフォルトのマップがGoogle mapではなく、
悪名高いApple map。
これでかのトコナメを見てみると…

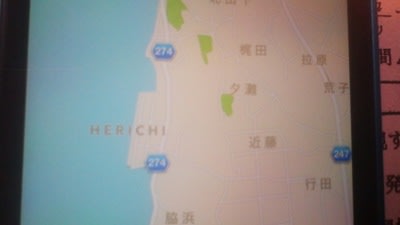
HERICHIｗｗｗｗｗ
何故ローマ字ｗｗｗ
どうやらトコナメ語は不完全にしか文字を持たないので
アルファベットで表音表記しているようですね。

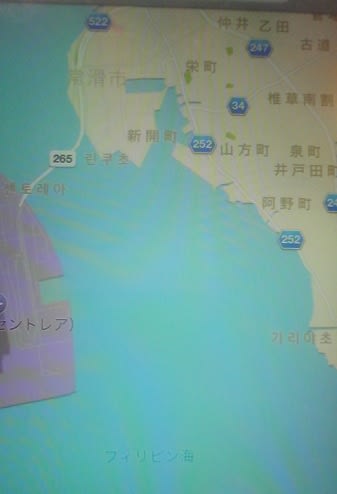
そして、トコナメ語は日本語とは文字が若干違うようです。
あと、トコナメはフィリピン海に浮かんでいるそうです。
トコナメの謎は計り知れません。

…最初にダウンロードしたアプリが
「Google Maps」であった事は言うまでもない。

まだ気付いていないのか…
大多数の日本人がクリスマスを祝うというのは
如何に恐ろしく、世紀末的な事であるかに…！
実は、日本人がクリスマスを祝うと、
何をしても許される無法状態になってしまうのです。
それを論理学的に証明してみせましょう。

まずは記号の説明から。
￢…～でない（not）
⇒…ならば（then）
∧…かつ（and）
∨…または（or）
∀…全ての～について（for all）
∃…ある～について（exsit）

さて、命題Pを
「日本人の大半はキリスト教徒である」
とします。
日本人の内キリスト教を信仰している人は
全人口の3％にも満ちませんから、
当然￢Pが真となります。
しかし、キリスト降誕祭たるクリスマスを祝うのは
当然キリスト教徒に限られる訳ですから、
日本人の大半がクリスマスを祝うというのは
￢P∧P（日本人はキリスト教徒でないと同時に
キリスト教徒である）を意味します。

次に、Q(n)を「～をしても良い」とし、
n=1,2,…として、あらゆる行為の是非を表します。
Q(n)にはあらゆる行為が含まれますから、
この中のとあるnには「殺人をしても良い」など
明らかに偽である命題も必ず含まれています。
即ち、この命題の内一つをQ(a)とすると、￢Q(a)は真。

公理A(t)⇒∃xA(x)に於いて、
A(t)に￢Q(a)を、xにnを代入すると、
￢Q(a)⇒∃n￢Q(n)…①

公理∃xA(x)⇔￢(∀x￢A(x))に於いて、
A(x)に￢Q(n)を代入すると、
∃n￢Q(n)⇒￢(∀n￢￢Q(n))

公理￢￢A⇒Aより、
∃n￢Q(n)⇒￢(∀nQ(n))…②

①、②より、
￢Q(a)⇒￢(∀nQ(n))

ここで、￢Q(a)は真なので、
￢(∀nQ(n))（全ての行為をして良い訳ではない）
が真となります。

また、ω無矛盾性より、∀A￢(A∧￢A)
（どんな命題でも、真かつ偽である事はない）
も真となっています。
￢(∀nQ(n))と∀A￢(A∧￢A)は互いに独立して真なので、
￢(∀nQ(n))⇒∀A￢(A∧￢A)

この対偶をとると、
￢∀A￢(A∧￢A)⇒￢￢(∀nQ(n))

公理∃xA(x)⇔￢(∀x￢A(x))、公理￢￢A⇒Aより、
∃A(A∧￢A)⇒∀nQ(n)…③

ここで、日本人の大半がクリスマスを祝うと
￢P∧Pが成り立ってしまうので、
∃A(A∧￢A)が真となります。
すると、③より∀nQ(n)、
即ち「全ての行為はしても良い」が真となります。 Q.E.D.

…正直、疲れました。
何か小難しい事をやっているように見えますが、
1つ1つの段階で言っていることは当たり前すぎて
だから何？と思ってしまうような事ばかりです。
ちなみに、これは詭弁ではなく論理学的に本当に正しい論法です。
それなのに何故こんな結論が導かれるのかというと、
たった1点だけ間違っている点があるから。
そう、
「大多数の日本人がクリスマスを祝う」
というこの点です。
皆さんもクリスマスを祝う時は気を付けましょう。
それでは。

メリークリスマス！