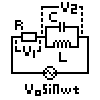
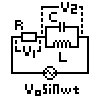
金曜日の物理の授業で出てきたRLC回路。
(以前のホイートストンブリッジの時に、
「携帯電話だと小さくて見えない。」
という声があったので、今回は大きくしてみました。)
「直列だと電圧を出すには微分方程式が要るけど、
高校生だと数学が追い付かないから無理だねー(チラッ」
と喧嘩を売られた気がしたので、
上等だ!売られた喧嘩は買ってやんよ!
という事で40分掛けて解いてみました。
計算を進めれば進めるほど複雑になっていく式を前に、
挫折しかけつつ、やっとの思いで出てきた解がこちら。
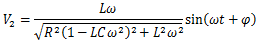
但し、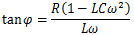
かなり複雑です。
ホイートストンブリッジの比ではありません。
…そうですね。
数学に通じている人なら気付きましたね。
そう、微分方程式の解であるにも関わらず
任意定数を1つも含んでいないこの解は
一般解ではなく特殊解に過ぎないのです。
…ここまできたらやるか!
という訳で更に30分かけて出した一般解がこちら。
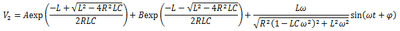
A、Bは任意の実数です。
exp(x)というのはexのこと。
まともにeの肩に乗せると物凄く見辛いので…
乗せるとこんな感じ。
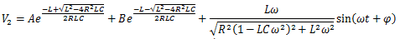
ここまでくるとR-16Gくらいのグロテスクさですね。
本当はL2-4R2LCの正負で場合分けして
過減衰、臨界減衰、減衰振動に分けるのですが、
その辺りは勘弁して下さい…
一応、オイラーの公式的には包括された解なので。
自分でも解いてみたくなったそこの貴方に大ヒント!
この微分方程式を解けば出ます。
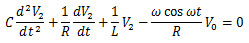
非同次線形2階微分方程式なので、
現在302の後ろの黒板に書いてある微分方程式
(同次線形1階微分方程式)より2ランクほど上です。
お試しあれ。


コメント